5.7 GLMakie.jl

CairoMakie.jl fornece todas as nossas necessidades de imagens 2D estáticas. Mas às vezes queremos interatividade, principalmente quando estamos lidando com imagens 3D. A visualização de dados em 3D também é uma prática comum para obter insights de seus dados. É aqui que GLMakie.jl pode ser útil, já que usa OpenGL como um backend que adiciona interatividade e capacidade de resposta a plots. Como antes, um plot simples inclui, é claro, linhas e pontos. Então, vamos começar com eles e como já sabemos como os layouts funcionam, vamos colocar isso em prática.

5.7.1 Dispersão e Linhas

Para os gráficos de dispersão temos duas opções, a primeira é scatter(x, y, z) e a segunda é meshscatter(x, y, z). Na primeira, os marcadores não são escalonados nas direções dos eixos, mas na segunda, porque são geometrias reais no espaço 3D. Veja o próximo exemplo:

using GLMakie
GLMakie.activate!()

function scatters_in_3D()
    seed!(123)
    xyz = randn(10, 3)
    x, y, z = xyz[:, 1], xyz[:, 2], xyz[:, 3]
    fig = Figure(resolution=(1600, 400))
    ax1 = Axis3(fig[1, 1]; aspect=(1, 1, 1), perspectiveness=0.5)
    ax2 = Axis3(fig[1, 2]; aspect=(1, 1, 1), perspectiveness=0.5)
    ax3 = Axis3(fig[1, 3]; aspect=:data, perspectiveness=0.5)
    scatter!(ax1, x, y, z; markersize=50)
    meshscatter!(ax2, x, y, z; markersize=0.25)
    hm = meshscatter!(ax3, x, y, z; markersize=0.25,
        marker=FRect3D(Vec3f(0), Vec3f(1)), color=1:size(xyz)[2],
        colormap=:plasma, transparency=false)
    Colorbar(fig[1, 4], hm, label="values", height=Relative(0.5))
    fig
end
scatters_in_3D()

Observe também que uma geometria diferente pode ser passada como marcadores, ou seja, um quadrado/ângulo e podemos atribuir-lhes uma colormap também. No painel central, pode-se obter esferas perfeitas fazendo aspect = :data como no painel direito.

E fazendo lines ou scatterlines é também bem simples:

function lines_in_3D()
    seed!(123)
    xyz = randn(10, 3)
    x, y, z = xyz[:, 1], xyz[:, 2], xyz[:, 3]
    fig = Figure(resolution=(1600, 400))
    ax1 = Axis3(fig[1, 1]; aspect=(1, 1, 1), perspectiveness=0.5)
    ax2 = Axis3(fig[1, 2]; aspect=(1, 1, 1), perspectiveness=0.5)
    ax3 = Axis3(fig[1, 3]; aspect=:data, perspectiveness=0.5)
    lines!(ax1, x, y, z; color=1:size(xyz)[2], linewidth=3)
    scatterlines!(ax2, x, y, z; markersize=50)
    hm = meshscatter!(ax3, x, y, z; markersize=0.2, color=1:size(xyz)[2])
    lines!(ax3, x, y, z; color=1:size(xyz)[2])
    Colorbar(fig[2, 1], hm; label="values", height=15, vertical=false,
        flipaxis=false, ticksize=15, tickalign=1, width=Relative(3.55 / 4))
    fig
end
lines_in_3D()

Plotando uma surface também é fácil de ser fazer assim como um wireframe e linhas contour em 3D.

5.7.2 surfaces, wireframe, contour, contourf e contour3d

Para mostrar estes casos, utilizaremos a seguinte função peaks:

function peaks(; n=49)
    x = LinRange(-3, 3, n)
    y = LinRange(-3, 3, n)
    a = 3 * (1 .- x') .^ 2 .* exp.(-(x' .^ 2) .- (y .+ 1) .^ 2)
    b = 10 * (x' / 5 .- x' .^ 3 .- y .^ 5) .* exp.(-x' .^ 2 .- y .^ 2)
    c = 1 / 3 * exp.(-(x' .+ 1) .^ 2 .- y .^ 2)
    return (x, y, a .- b .- c)
end

A saída para as diferentes funções de plotagem é:

function plot_peaks_function()
    x, y, z = peaks()
    x2, y2, z2 = peaks(; n=15)
    fig = Figure(resolution=(1600, 400), fontsize=26)
    axs = [Axis3(fig[1, i]; aspect=(1, 1, 1)) for i = 1:3]
    hm = surface!(axs[1], x, y, z)
    wireframe!(axs[2], x2, y2, z2)
    contour3d!(axs[3], x, y, z; levels=20)
    Colorbar(fig[1, 4], hm, height=Relative(0.5))
    fig
end
plot_peaks_function()

Mas, também pode ser plotado com um heatmap(x, y, z), contour(x, y, z) ou contourf(x, y, z):

function heatmap_contour_and_contourf()
    x, y, z = peaks()
    fig = Figure(resolution=(1600, 400), fontsize=26)
    axs = [Axis(fig[1, i]; aspect=DataAspect()) for i = 1:3]
    hm = heatmap!(axs[1], x, y, z)
    contour!(axs[2], x, y, z; levels=20)
    contourf!(axs[3], x, y, z)
    Colorbar(fig[1, 4], hm, height=Relative(0.5))
    fig
end
heatmap_contour_and_contourf()

Adicionalmente, ao mudarmos Axis para um Axis3, estes plots estarão automaticamente no plano x-y:

function heatmap_contour_and_contourf_in_a_3d_plane()
    x, y, z = peaks()
    fig = Figure(resolution=(1600, 400), fontsize=26)
    axs = [Axis3(fig[1, i]) for i = 1:3]
    hm = heatmap!(axs[1], x, y, z)
    contour!(axs[2], x, y, z; levels=20)
    contourf!(axs[3], x, y, z)
    Colorbar(fig[1, 4], hm, height=Relative(0.5))
    fig
end
heatmap_contour_and_contourf_in_a_3d_plane()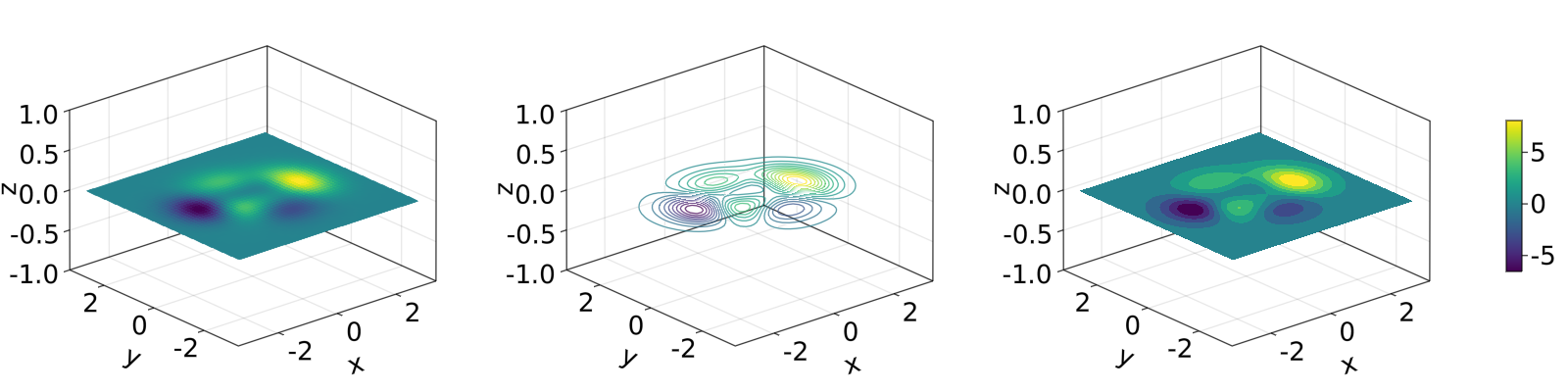

Algo que também é bem facil de fazer é misturar todas essas fun;óes de plotagens em um único plot:

using TestImages

function mixing_surface_contour3d_contour_and_contourf()
    img = testimage("coffee.png")
    x, y, z = peaks()
    cmap = :Spectral_11
    fig = Figure(resolution=(1200, 800), fontsize=26)
    ax1 = Axis3(fig[1, 1]; aspect=(1, 1, 1), elevation=pi / 6, xzpanelcolor=(:black, 0.75),
        perspectiveness=0.5, yzpanelcolor=:black, zgridcolor=:grey70,
        ygridcolor=:grey70, xgridcolor=:grey70)
    ax2 = Axis3(fig[1, 3]; aspect=(1, 1, 1), elevation=pi / 6, perspectiveness=0.5)
    hm = surface!(ax1, x, y, z; colormap=(cmap, 0.95), shading=true)
    contour3d!(ax1, x, y, z .+ 0.02; colormap=cmap, levels=20, linewidth=2)
    xmin, ymin, zmin = minimum(ax1.finallimits[])
    xmax, ymax, zmax = maximum(ax1.finallimits[])
    contour!(ax1, x, y, z; colormap=cmap, levels=20, transformation=(:xy, zmax))
    contourf!(ax1, x, y, z; colormap=cmap, transformation=(:xy, zmin))
    Colorbar(fig[1, 2], hm, width=15, ticksize=15, tickalign=1, height=Relative(0.35))
    # transformations into planes
    heatmap!(ax2, x, y, z; colormap=:viridis, transformation=(:yz, 3.5))
    contourf!(ax2, x, y, z; colormap=:CMRmap, transformation=(:xy, -3.5))
    contourf!(ax2, x, y, z; colormap=:bone_1, transformation=(:xz, 3.5))
    image!(ax2, -3 .. 3, -3 .. 2, rotr90(img); transformation=(:xy, 3.8))
    xlims!(ax2, -3.8, 3.8)
    ylims!(ax2, -3.8, 3.8)
    zlims!(ax2, -3.8, 3.8)
    fig
end
mixing_surface_contour3d_contour_and_contourf()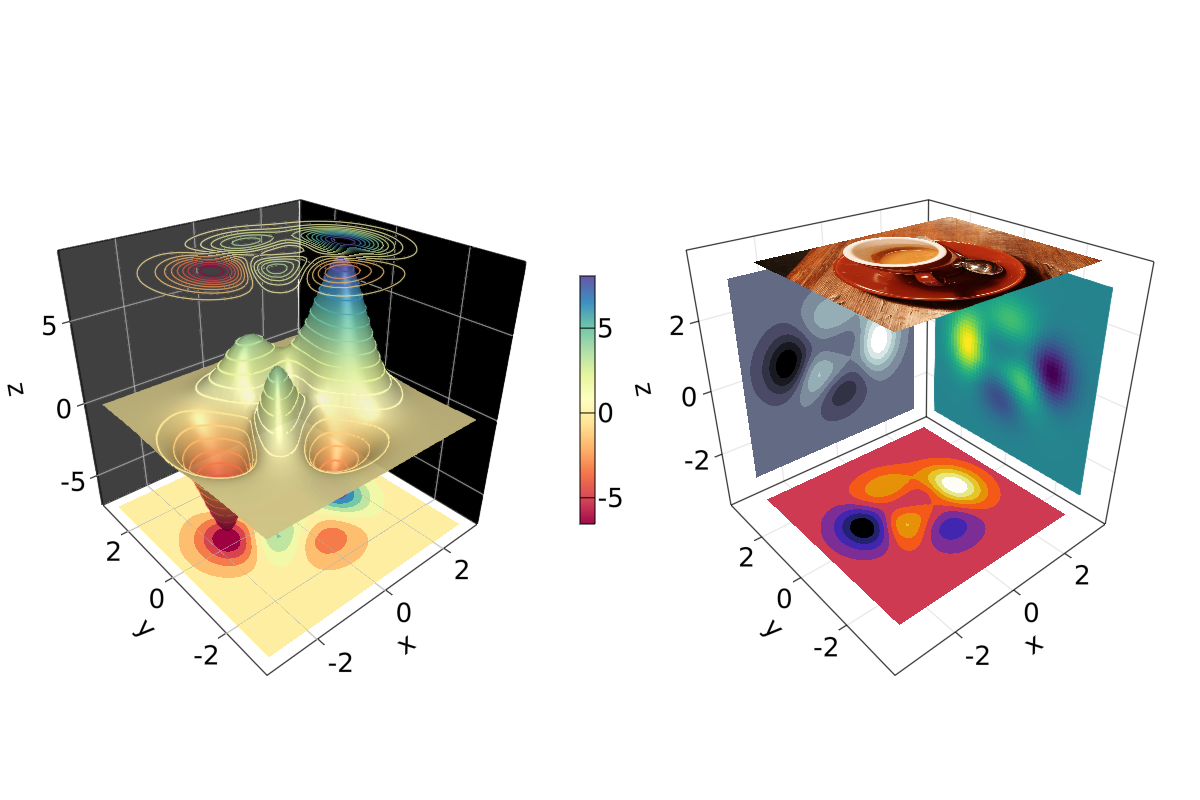

Não é ruim, certo? É claro que qualquer heatmaps, contours, contourfs ou image pode ser plotado em qualquer plot.

5.7.3 arrows e streamplots

arrows e streamplot são plots que podem ser úteis quando queremos saber as direções que uma determinada variável seguirá. Veja uma demonstração abaixo¹⁸:

using LinearAlgebra

function arrows_and_streamplot_in_3d()
    ps = [Point3f(x, y, z) for x = -3:1:3 for y = -3:1:3 for z = -3:1:3]
    ns = map(p -> 0.1 * rand() * Vec3f(p[2], p[3], p[1]), ps)
    lengths = norm.(ns)
    flowField(x, y, z) = Point(-y + x * (-1 + x^2 + y^2)^2, x + y * (-1 + x^2 + y^2)^2,
        z + x * (y - z^2))
    fig = Figure(resolution=(1200, 800), fontsize=26)
    axs = [Axis3(fig[1, i]; aspect=(1, 1, 1), perspectiveness=0.5) for i = 1:2]
    arrows!(axs[1], ps, ns, color=lengths, arrowsize=Vec3f0(0.2, 0.2, 0.3),
        linewidth=0.1)
    streamplot!(axs[2], flowField, -4 .. 4, -4 .. 4, -4 .. 4, colormap=:plasma,
        gridsize=(7, 7), arrow_size=0.25, linewidth=1)
    fig
end
arrows_and_streamplot_in_3d()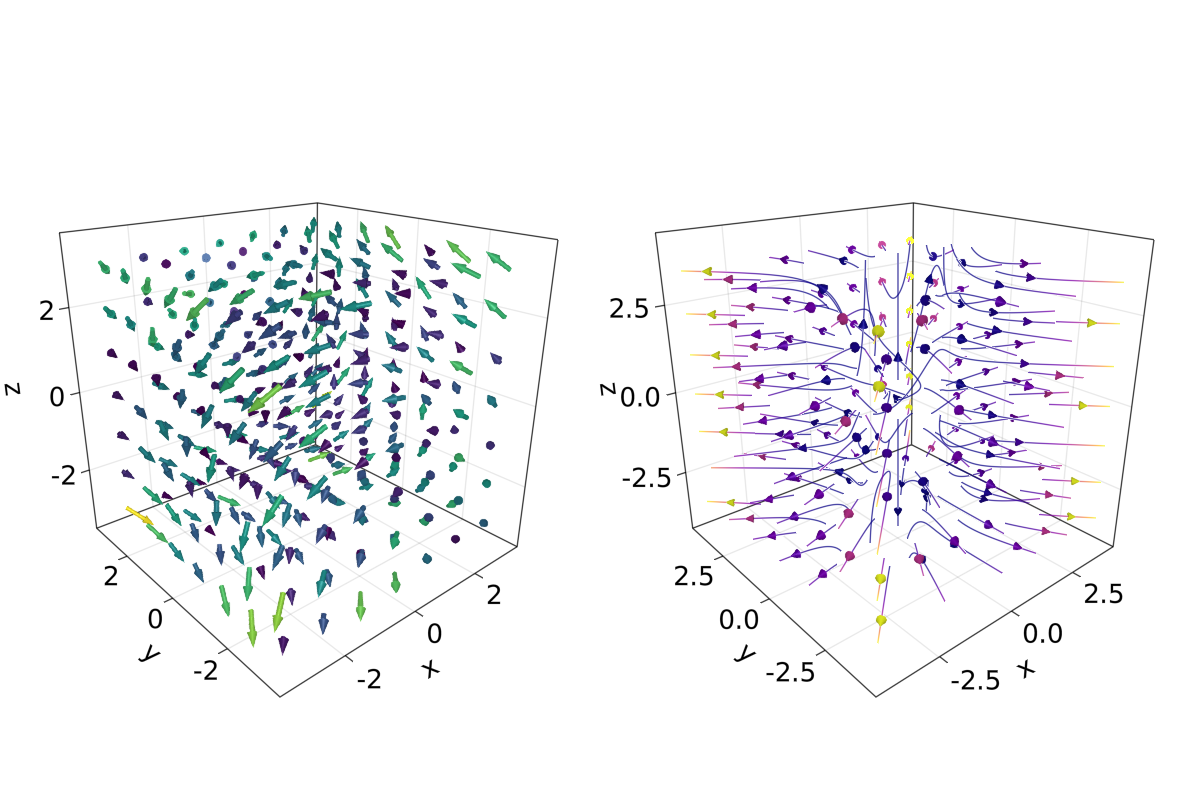

Outros exemplos interessantes são mesh(obj), volume(x, y, z, vals), e contour(x, y, z, vals).

5.7.4 Mesh e Volumes

Visualizações de mesh são úteis quando você quer plotar geometrias, como uma Sphere ou um Retângulo, ex: FRect3D. Outra abordagem para visualizar pontos no espaço 3D é chamando as funções volume e contour, que implementam ray tracing para simular uma grande variedade de efeitos ópticos. Veja os próximos exemplos:

using GeometryBasics

function mesh_volume_contour()
    # mesh objects
    rectMesh = FRect3D(Vec3f(-0.5), Vec3f(1))
    recmesh = GeometryBasics.mesh(rectMesh)
    sphere = Sphere(Point3f(0), 1)
    # https://juliageometry.github.io/GeometryBasics.jl/stable/primitives/
    spheremesh = GeometryBasics.mesh(Tesselation(sphere, 64))
    # uses 64 for tesselation, a smoother sphere
    colors = [rand() for v in recmesh.position]
    # cloud points for volume
    x = y = z = 1:10
    vals = randn(10, 10, 10)
    fig = Figure(resolution=(1600, 400))
    axs = [Axis3(fig[1, i]; aspect=(1, 1, 1), perspectiveness=0.5) for i = 1:3]
    mesh!(axs[1], recmesh; color=colors, colormap=:rainbow, shading=false)
    mesh!(axs[1], spheremesh; color=(:white, 0.25), transparency=true)
    volume!(axs[2], x, y, z, vals; colormap=Reverse(:plasma))
    contour!(axs[3], x, y, z, vals; colormap=Reverse(:plasma))
    fig
end
mesh_volume_contour()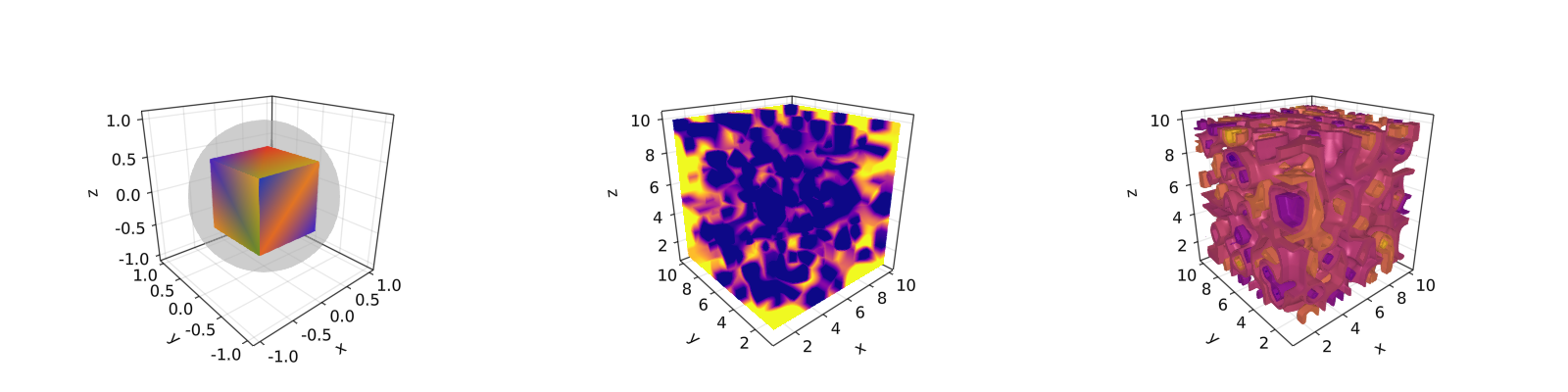

Note que aqui estamos traçando duas mesh no mesmo eixo, uma esfera transparente e um cubo. Até agora, cobrimos a maioria dos casos de uso 3D. Outro exemplo é ?linesegments.

Tomando como referência o exemplo anterior, pode-se fazer o seguinte plot personalizado com esferas e retângulos:

using GeometryBasics, Colors

Para as esferas, vamos fazer um grid retangular. Além disso, usaremos uma cor diferente para cada uma delas. Adicionalmente, podemos misturar esferas e um plano retangular. Em seguida, definimos todos os dados necessários.

seed!(123)
spheresGrid = [Point3f(i,j,k) for i in 1:2:10 for j in 1:2:10 for k in 1:2:10]
colorSphere = [RGBA(i * 0.1, j * 0.1, k * 0.1, 0.75) for i in 1:2:10 for j in 1:2:10 for k in 1:2:10]
spheresPlane = [Point3f(i,j,k) for i in 1:2.5:20 for j in 1:2.5:10 for k in 1:2.5:4]
cmap = get(colorschemes[:plasma], LinRange(0, 1, 50))
colorsPlane = cmap[rand(1:50,50)]
rectMesh = FRect3D(Vec3f(-1, -1, 2.1), Vec3f(22, 11, 0.5))
recmesh = GeometryBasics.mesh(rectMesh)
colors = [RGBA(rand(4)...) for v in recmesh.position]

Então, o plot é feito simplesmente com:

function grid_spheres_and_rectangle_as_plate()
    fig = with_theme(theme_dark()) do
        fig = Figure(resolution=(1200, 800))
        ax1 = Axis3(fig[1, 1]; aspect=:data, perspectiveness=0.5, azimuth=0.72)
        ax2 = Axis3(fig[1, 2]; aspect=:data, perspectiveness=0.5)
        meshscatter!(ax1, spheresGrid; color = colorSphere, markersize = 1,
            shading=false)
        meshscatter!(ax2, spheresPlane; color=colorsPlane, markersize = 0.75,
            lightposition=Vec3f(10, 5, 2), ambient=Vec3f(0.95, 0.95, 0.95),
            backlight=1.0f0)
        mesh!(recmesh; color=colors, colormap=:rainbow, shading=false)
        limits!(ax1, 0, 10, 0, 10, 0, 10)
        fig
    end
    fig
end
grid_spheres_and_rectangle_as_plate()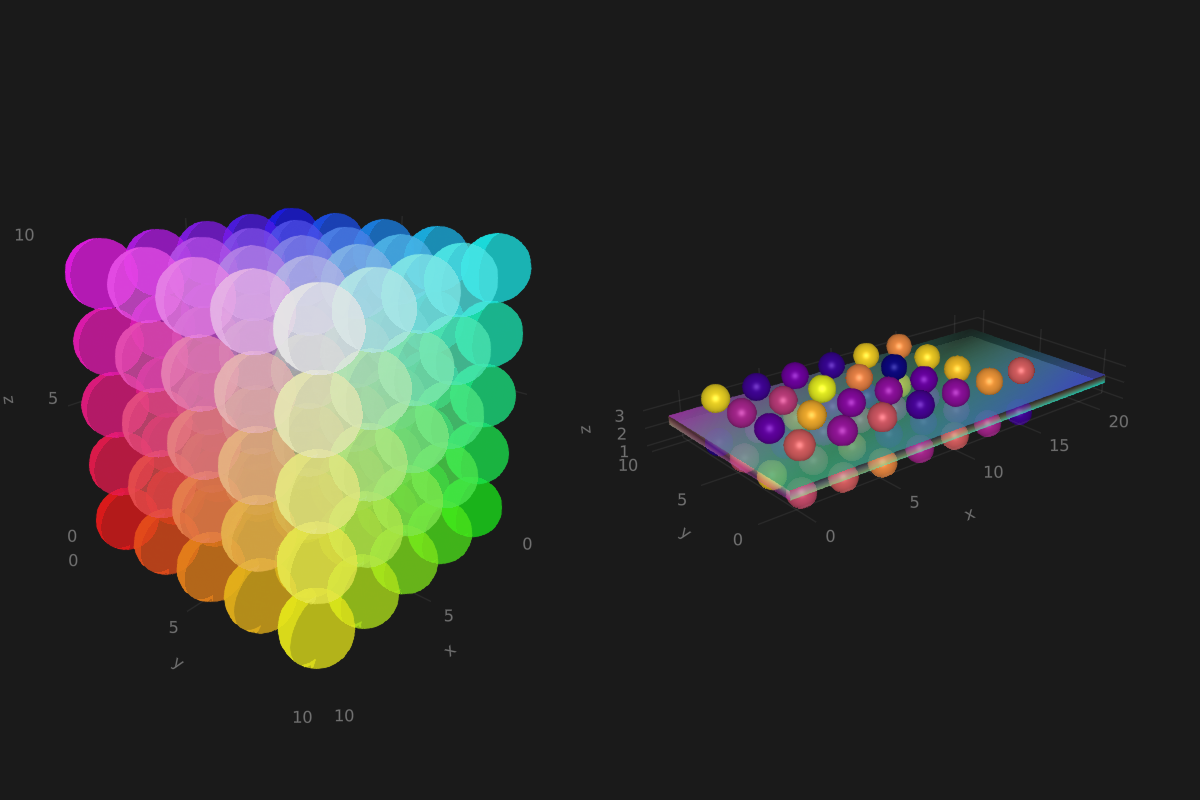

Aqui, o retângulo é semi-transparente devido ao canal alfa adicionado à cor RGB. A função de retângulo é bastante versátil, por exemplo, box 3D é fácil implementar que por sua vez pode ser usada para traçar um histograma 3D. Veja nosso próximo exemplo, onde estamos usando novamente nossa função peaks e algumas definições adicionais:

x, y, z = peaks(; n=15)
δx = (x[2] - x[1]) / 2
δy = (y[2] - y[1]) / 2
cbarPal = :Spectral_11
ztmp = (z .- minimum(z)) ./ (maximum(z .- minimum(z)))
cmap = get(colorschemes[cbarPal], ztmp)
cmap2 = reshape(cmap, size(z))
ztmp2 = abs.(z) ./ maximum(abs.(z)) .+ 0.15

aqui \(\delta x, \delta y\) são usados para especificar o tamanho das box. cmap2 será a cor de cada box e ztmp2 será usado como o parâmetro de transparência. Veja o resultado na próxima figura.

function histogram_or_bars_in_3d()
    fig = Figure(resolution=(1200, 800), fontsize=26)
    ax1 = Axis3(fig[1, 1]; aspect=(1, 1, 1), elevation=π/6,
        perspectiveness=0.5)
    ax2 = Axis3(fig[1, 2]; aspect=(1, 1, 1), perspectiveness=0.5)
    rectMesh = FRect3D(Vec3f0(-0.5, -0.5, 0), Vec3f0(1, 1, 1))
    meshscatter!(ax1, x, y, 0*z, marker = rectMesh, color = z[:],
        markersize = Vec3f.(2δx, 2δy, z[:]), colormap = :Spectral_11,
        shading=false)
    limits!(ax1, -3.5, 3.5, -3.5, 3.5, -7.45, 7.45)
    meshscatter!(ax2, x, y, 0*z, marker = rectMesh, color = z[:],
        markersize = Vec3f.(2δx, 2δy, z[:]), colormap = (:Spectral_11, 0.25),
        shading=false, transparency=true)
    for (idx, i) in enumerate(x), (idy, j) in enumerate(y)
        rectMesh = FRect3D(Vec3f(i - δx, j - δy, 0), Vec3f(2δx, 2δy, z[idx, idy]))
        recmesh = GeometryBasics.mesh(rectMesh)
        lines!(ax2, recmesh; color=(cmap2[idx, idy], ztmp2[idx, idy]))
    end
    fig
end
histogram_or_bars_in_3d()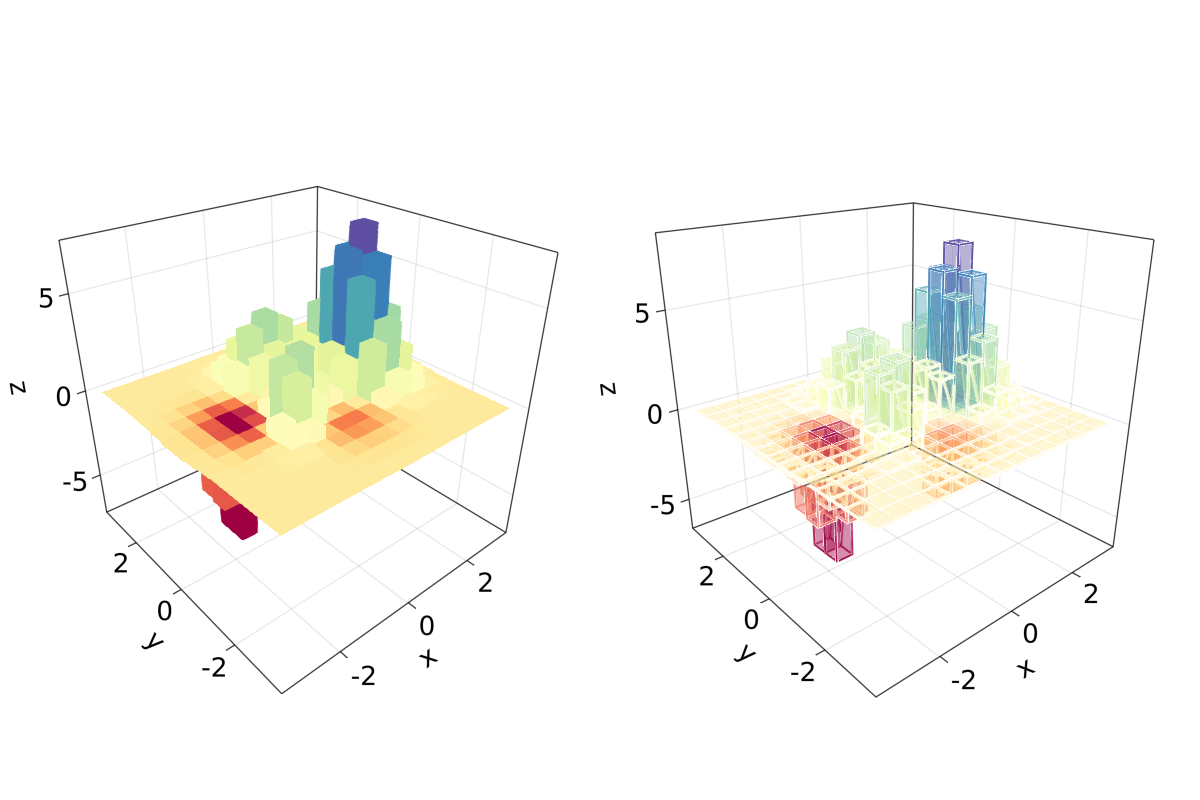

Note que você pode também usar lines ou wireframe sobre um objeto mesh.

5.7.5 Linhas Preenchidas e band

Para o nosso último exemplo vamos mostrar como fazer uma curva preenchida em 3d com band e alguns linesegments:

function filled_line_and_linesegments_in_3D()
    xs = LinRange(-3, 3, 10)
    lower = [Point3f(i, -i, 0) for i in LinRange(0, 3, 100)]
    upper = [Point3f(i, -i, sin(i) * exp(-(i + i))) for i in range(0, 3, length=100)]
    fig = Figure(resolution=(1200, 800))
    axs = [Axis3(fig[1, i]; elevation=pi/6, perspectiveness=0.5) for i = 1:2]
    band!(axs[1], lower, upper, color=repeat(norm.(upper), outer=2), colormap=:CMRmap)
    lines!(axs[1], upper, color=:black)
    linesegments!(axs[2], cos.(xs), xs, sin.(xs), linewidth=5, color=1:length(xs))
    fig
end
filled_line_and_linesegments_in_3D()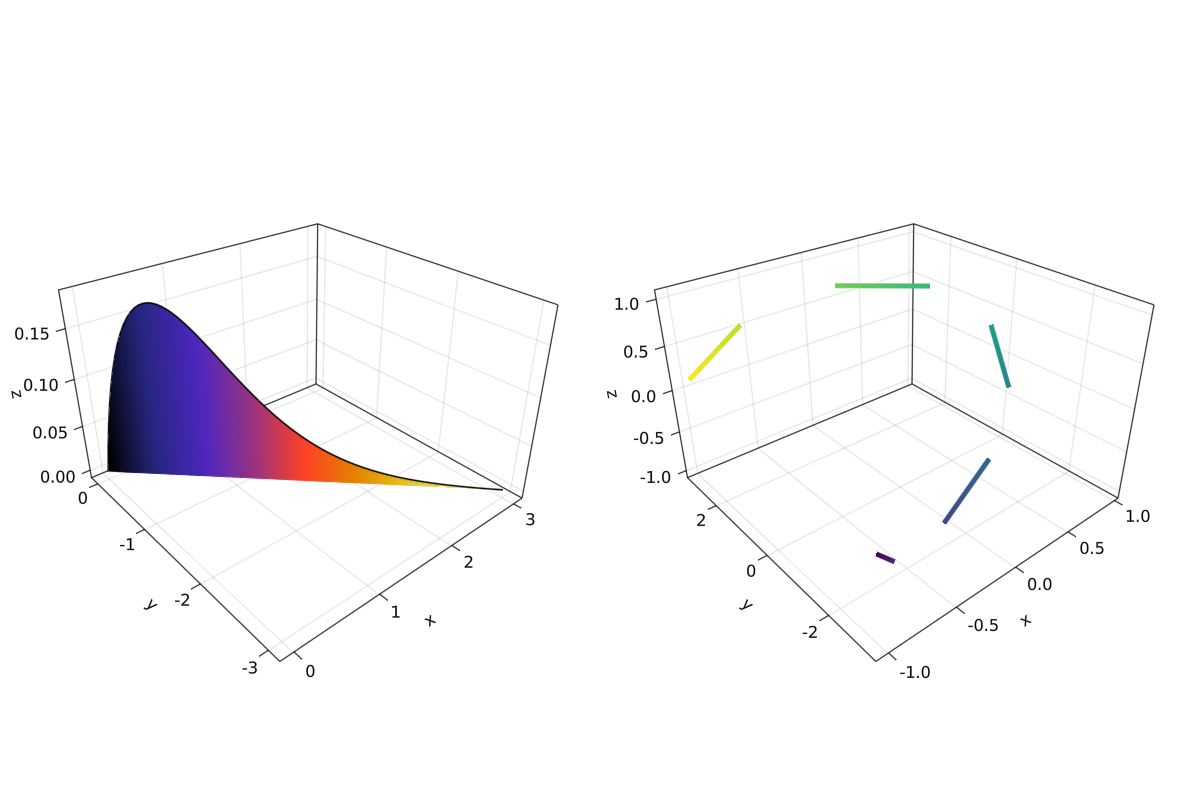

Finalmente, nossa jornada fazendo plots 3D chegou ao fim. Você pode combinar tudo o que expostos aqui para criar imagens 3D incríveis!

---

1. 18. Estamos usando o módulo LinearAlgebra da biblioteca padrão de Julia.↩︎